Understanding the microstructural features of polycrystalline materials (see top figure) such as high-performance ceramics (HPCs) is a prerequisite for the design of materials with desired superior properties, such as high toughness or strength. On the length scale of a few microns to a few hundreds of microns, many materials exhibit a polyhedral granular structure which is known to crucially influence their macroscopic mechanical properties. With ceramics, the specific shape and size of these polycrystalline grain structures is formed during a sintering process where atomic diffusion plays a dominant role.
Usually, the sintering process results in a dense microstructure with grain sizes of several hundreds of micrometers. Using a nanosized fine-grained granulate as a green body along with an adequate process control it is possible to minimize both, the porosity 0.05% in volume, as well as the generated average grain size (smaller than 1 μm). It is known that both leads to a dramatic increase in hardness which outperforms most metal alloys at considerably lower weight. It is striking that producing very small grain sizes in the making of HPCs below 50 μm results again in decreasing hardness. Hence, there is no simple connection between grain size and hardness of a polycrystalline material. Today, one is compelled to search for the optimal micro-structure for a specific application by intricate and expensive experimental “trial-and-error” studies. In order to overcome this situation by numerical simulations, a detailed and realistic modeling of the available experimental structures is a basic requirement. With numerical investigations taking explicitly into account the microstructural details (see second figure from top), one can expect to achieve a considerably enhanced understanding of the structure-property relationships of such materials.
Whether a material under compressive or tensile load exhibits brittle behavior or ductility depends upon the underlying crystal structure and the propagation of defects in the respective material. On an atomic scale, dislocations and initial imperfections in the crystal structure are the origin of the mechanical behavior of materials on a macroscopic length scale. On a length scale of microns the principal units of a brittle material are polycrystals which usually have a polyhedral structure and which presumably determine many macroscopic properties. Despite the ever growing computational prospects, atomistic simulations taking into account the interaction between billions of atoms are still not capable of resolving physical phenomena on length- and time scales as observed in experiments.
This fact justifies modelling physical systems specifically on mesoscopic length scales. We pursue two basic approaches. On the one hand, the material can be approximated by particles, the size of which can be varied. Depending on the size of the particles, the system resolution varies between 0.01-1000 μm (see third figure from top). The interaction is described by potentials which can ultimately motivated by Quantum Theory. Thus, it is possible to model cohesion and repulsion as the two key properties of a macroscopic solid state, based on physical principles on a mesoscopic level. The particles are propagated through time by means of Molecular Dynamics techniques (in this context often called Discrete Element Method (DEM)) which are implemented in the Code MD-Cube. Fracture propagation can be studied in detail as well as the impact dynamics of solid states.
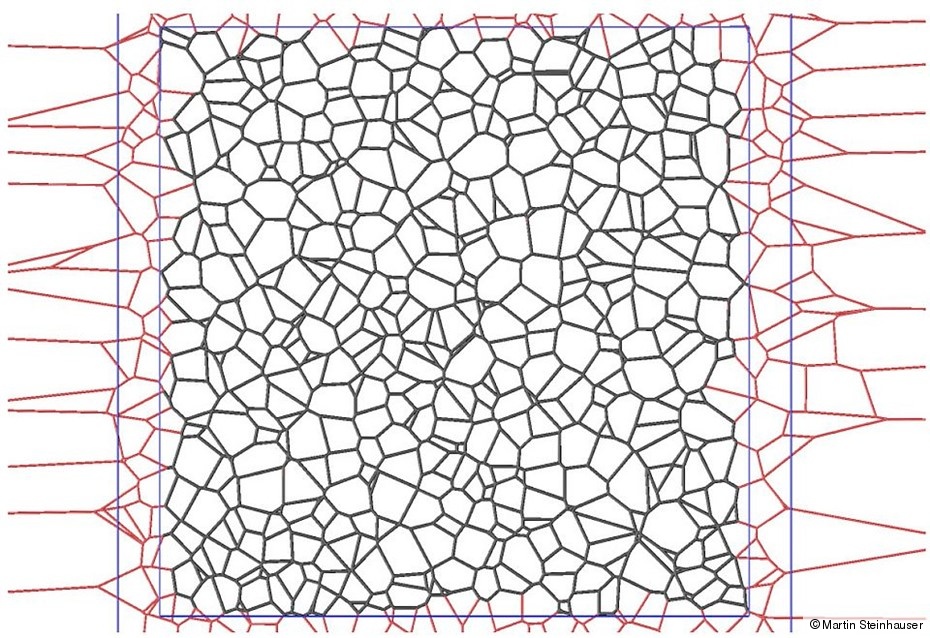
Alternatively, we use a standard Finite Element approach for modeling the mesoscopic grain structure, where the individual grains are modeled using a continuum approximation. In this case the grains’ cohesive properties at interfaces have to be modeled separately. Different statistical realizations of grain structures based on power diagrams (which are an extension of the ordinary Voronoi diagram in 3D to N dimensions) and their influence on the macroscopic properties of the material specimen can be analyzed by this numerical technique (see bottom figure) which shows a 2-dimensional cut through a power diagram in 3 dimensions. This cut constitutes the same statistical information on the granular microstructure as the one found in polished micrographs (see top figure). Evaluating the statistics of the cut through the power diagram, i.e. evaluating the first 4 or 5 moments and comparing the results with the corresponding quantities obtained from experimental micrographs, we optimize our 3D polyhedral grain structures hich are the power diagrams) with a reverse Monte-Carlo procedure until the statistical moments in both structures agree with each other beyond a certain error limit. For calculating the power diagrams we use a very efficient worst-case NlogN-algorithm.
Selected publications
Modeling and Simulation of Microstructures using Power Diagrams: Proof of Concept
M. Kühn, M.O. Steinhauser
Appl. Phys. Lett. 2008, 93, 1