Multiscale Materials Modeling

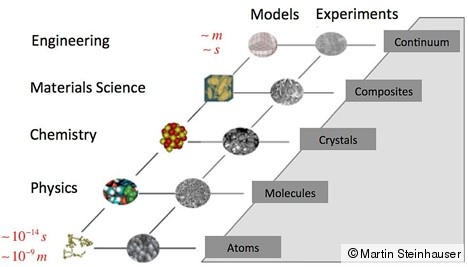
The observed properties of solids and structures are only the macroscopic manifestation of very many complex interaction mechanisms involving structural components on numerous scales smaller than those we perceive with the naked eye (see Figure 1). A material can be, e.g., crystalline or amorphous, pure or alloyed, single- or multi-phase, single-crystal or polycrystalline; and every such information about the material's structure entails a significant impact on the overall material properties. The material's macroscopic properties comprise, e.g., the mechanical characteristics (such as the elastic moduli, the damping capacity, the hardening or softening behavior, the hardness, the toughness and ductility, or the fracture resistance), the electro-magnetic properties (the eletrical conductivity or the magnetic permeability, e.g.), the optical properties, the mass density, and many more physical specifics. All of these macrosopic material characteristicsstem from the material's composition across various scales. The interaction mechanisms on the different scales and their influence on the effective, macroscopic properties is of enormous importance to understand the material behavior and to design material behavior by demand.

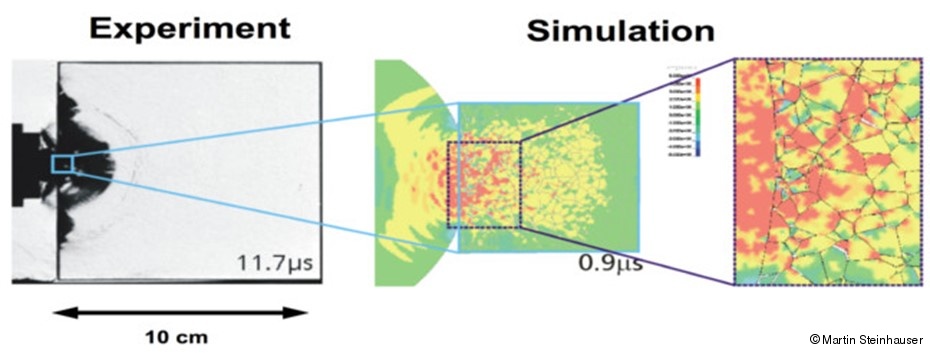
In Figure 2, the limitations of finite element approaches when trying to incorporate microstructural details of solids are displayed. The macroscopic specimen at the left cannot be modeled using finite elements when incorporating the granular microstructure because this leads to many hundreds of millions of elements. Thus, only a small fraction of the macroscopic specimen can be actually simulated with this approach. Such calculations are not feasible even on the largest computers due to great inefficiencies in the parallel implementation of algorithms in commercial FEM codes such as pamcrash, Autodyn, ANSYS, Lsdyna, to name but a few. Here, the limit due to the inefficiency of the implementation is usually reached with roughly 10 million elements, even on the largest computer systems. With self-written code this limit can be extended by a few million elements but the simulation of macroscopic bodies with microstructural features is still impossible. This calls for more sophisticated and more clever multiscale modeling and simulation methods that help bridging the scales.

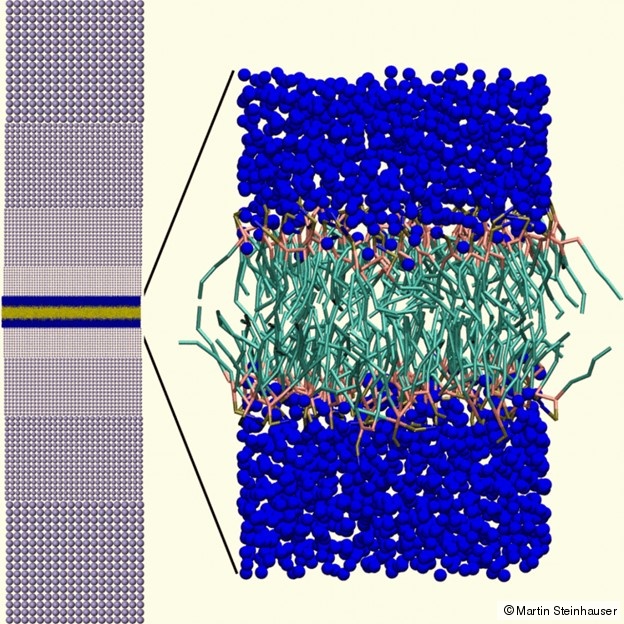
One example is our new multiscale simulation scheme which couples the atomic Molecular Dynamics (MD) method with a simulation method that is based on solving the conservation equations of the continuum, the Smooth Particle Hydrodynamics PH) method. We have proved that our coupling scheme works smoothly in both directions and show here a snapshot of a biomembrane where the aqueous environment is modeled as a continuum using a shock equation of state for water, while the membrane structure itself is resolved with great detail making use of a simplified coarse-grained model commonly used in polymer physics (see Figure 3).

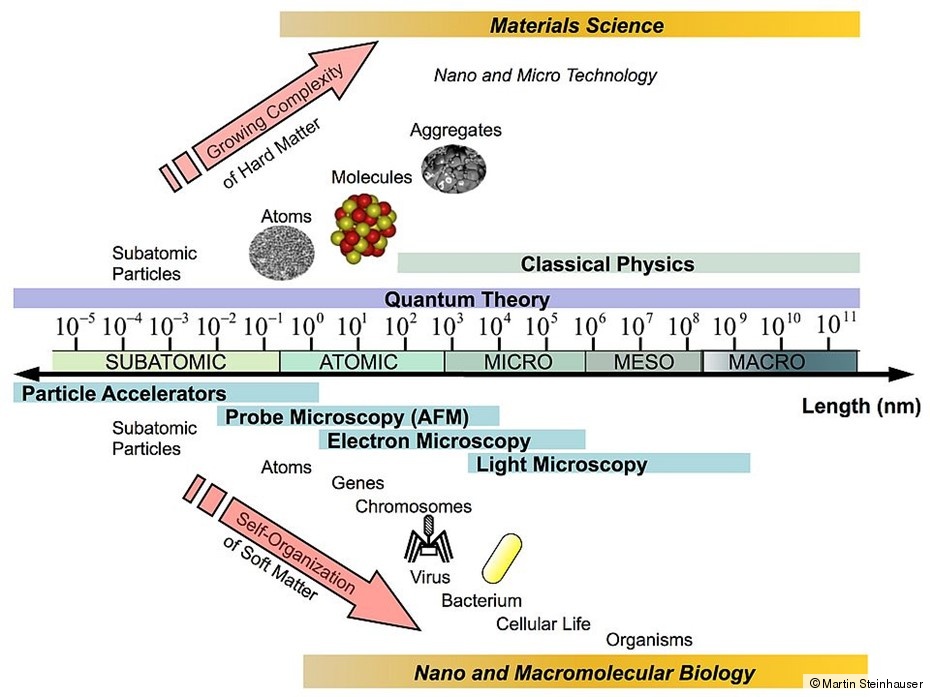
The relation of bridging the scales in the biological sciences (where nature does the upscaling based on the molecular machinery in the cells) and materials science (where scienctists try to bridge the scales either by miniaturization or by upscaling nano-devices) is displayed inFigure 4.